お知らせ
最小化法があまり使われないのはなぜか [J-CLEAR通信(69)]
確率割付についてレビューしたあとで最小化法の特徴を述べる。最小化法はあまり使用されないが,どのような場合に使うべきかを提案する。最小化法を含めた割付法については,総説1)~5)を参照されたい。
確率割付とは何か
比較試験では比較群への割付が必要となる。表1に示したように割付法は多くの種類があり,確率割付を伴う比較試験をランダム化比較試験(randomized controlled trial:RCT),そうでないものを非ランダム化試験(non-randomized trial)と呼ぶ。確率割付により割付群の比較可能性が高まり,内的妥当性が保証されるため,比較試験のゴールド・スタンダードはRCTだとされており,治療・予防効果を立証するほぼすべての臨床試験において,RCTが使用されている。

確率割付には3つの利点が知られている(表2)。1つは,確率を使って割り付けるので予見性が低く,選択バイアスが入りにくい点である。もう1つは,確率割付により観測された共変量のみならず,観測されていない因子までも,自動的に均衡化する点である。これにより,交絡バイアスが自動的に回避される。最後は,確率を用いて割付を行っているため,P値の計算を正当化してくれる点である。

Fisherは1935年に『実験計画法』6)を著し,実験の3原則を示した(表3)。ランダム化7),ブロック化,反復の3つである。ランダム化は確率割付のことであり,内的妥当性を保証する手法である。ブロック化は結果に強く影響する因子を制御する手法であり,層化法(あるいは層化割付)がそれに該当する。また,施設をブロックとして,ブロック内で同数ずつ割り付ける置換ブロック法8)という手法もある。

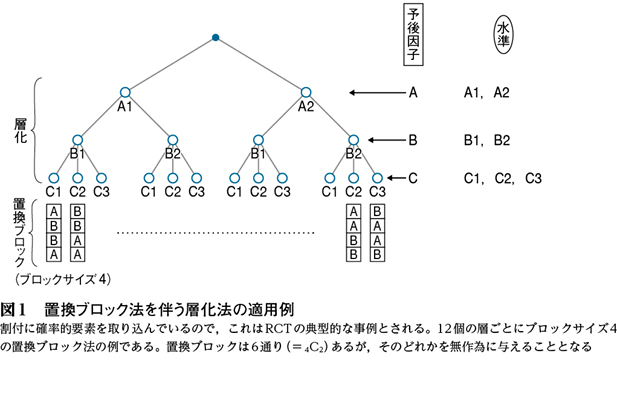
同時に適用することが多いため,permuted block within stratificationと呼ぶこともある。図1にその例を示した。各ブロックの4番目は決定論的になるが,それ以外は確率割付である。非予見性を高めるために,ブロックサイズを層ごとに,あるいは施設ごとに変えることもある。最後の反復により,見積もった測定誤差を用いた検定が可能になる。

残り3,011文字あります
会員登録頂くことで利用範囲が広がります。 » 会員登録する